Pythonは、今日最も人気のあるプログラミング言語の1つであり、さまざまなアプリケーションで使用されています。 2021年のStackOverflow開発者調査 によると、Pythonは依然として開発者の間で3番目に人気のあるプログラミング言語です。GitHub の 2021 年の State of the Octoverse レポートでは、Python が Javascript に次ぐ銀メダルを獲得しました。
その長年の人気のおかげで、開発者はWeb開発のために Flask、 Django、 FastAPI などの多くの人気のあるPythonフレームワークとライブラリを構築してきました。
ただし、PythonはWeb開発のためだけのものではありません。 これは、NumPy (数値Python)、Matplotlib、scikit-learn、PyTorchなどのライブラリやフレームワークを強化し、エンジニアリングや機械学習において極めて重要です。Pythonは、間違いなくAI、機械学習、データサイエンス開発のトップ言語です。 ディープラーニング(DL)の場合、 TensorFlow、PyTorch、 Keras などの主要なフレームワークはPythonフレンドリーです。
PyTorch と、線形回帰などの単純な問題に使用する方法を紹介します。 また、アプリケーションをコンテナー化する簡単な方法も提供します。 また、実際の問題とコンテナを介したデプロイについて深く掘り下げるパート2にも注目してください。 始めましょう。
PyTorchとは何ですか?
PyTorch の簡単な歴史と進化
Torchは、Lua言語で開発されたディープラーニングライブラリとして2002年にデビューしました。 したがって、Soumith ChintalaとAdam Paszke(どちらもMeta出身)は、2016年にPyTorchを開発し、Torchライブラリをベースにしています。 それ以来、開発者はそれに群がっています。 PyTorch は、 2021 年の StackOverflow 開発者調査で 3 番目に人気のあるフレームワークでした。 ただし、開発者の間で最も愛されているDLライブラリであり、人気は3位です。 Pytorchは、 テスラ、 ウーバー、 マイクロソフト、その他 7,300社以上が選択するDLフレームワークでもあります。
PyTorch は、GPU アクセラレーションによるテンソル計算に加えて、テープベースの自動グラード システム上に構築されたディープ ニューラル ネットワークを可能にします。 これらのテクノロジーについて学び始めたばかりの場合に備えて、これらの用語を簡単に説明します。
- 機械学習のコンテキストでは、テンソルは n 次元配列を指します。
- テープベースの自動グラードとは、Pytorchがコンピューターを使用して導関数(または勾配)を効果的に計算するための数学的手法である逆モード自動微分を使用することを意味します。
これらの数学に飛び込むには時間がかかりすぎる可能性があるため、詳細については次のリンクを確認してください。
PyTorch は膨大なライブラリであり、さまざまなディープ ラーニング アプリケーション向けの機能が豊富に含まれています。 はじめに、線形回帰のようなユースケースを評価しましょう。
線形回帰とは何ですか?
線形回帰は、最も一般的に使用される数学的モデリング手法の 1 つです。 2つの変数間の線形関係をモデル化します。 この手法は、2 つの変数間の相関関係を決定するのに役立ちます (または、独立変数の特定の値に基づいて値依存変数を決定します)。
機械学習では、線形回帰は多くの場合、予測および予測アプリケーションに適用されます。 通常はDLフレームワークを必要とせずに、分析的に解決できます。 ただし、これは PyTorch フレームワークを理解し、分析的な問題解決を開始するための良い方法です。
多数の書籍や Web リソースが線形回帰の理論を扱っています。 モデルの実装に役立つ十分な理論について説明します。 また、いくつかの重要な用語についても説明します。 さらに詳しく知りたい場合は、このセクションの最後にある有用なリソースを確認してください。
線形回帰モデル
基本的な線形回帰モデルは、次の式で表すことができます。
Y = mX + バイアス
各部分は何を表していますか?
- Y は従属変数で、ターゲットまたはラベルとも呼ばれます。
- X は独立変数で、特徴量または共変量とも呼ばれます。
- バイアスはオフセットとも呼ばれます。
- mは重量または「勾配」を指します。
これらの用語はしばしば交換可能です。 従属変数と独立変数は、スカラーまたはテンソルにすることができます。
線形回帰の目的は、既存のデータセットに基づく新しいデータ ポイントの予測でエラー率が最も低くなるように、重みとバイアスを選択することです。 簡単に言うと、線形回帰とは、データ分布に一致する最適な曲線(この場合は線)を見つけることです。
損失関数
損失関数は、実際の値と予測値の間の誤差(または損失)を表す誤差関数です。 損失を測定する非常に一般的な方法は、二乗平均平方根誤差を使用することです。
勾配降下アルゴリズム
勾配降下法は、重みとバイアスの最初の推測から始めて、(分析的またはディープラーニングモデルを使用して)問題を解決しようとする最適化アルゴリズムのクラスです。 次に、重みとバイアスの値を連続的に適切な推測で更新することにより、エラーを繰り返し削減します。
簡略化されたアプローチでは、損失関数の導関数を使用し、損失を最小限に抑えます。 導関数は数学的曲線の傾きであり、その底に到達しようとしているため、勾配降下法という名前が付けられています。 確率的勾配法は、データの小さなバッチをサンプリングして更新を計算するため、各反復でデータセット全体を渡すよりも計算上優れています。
この理論の詳細については、次のリソースが役立ちます。
ピトルチによる線形回帰
次に、PyTorch を使用した線形回帰モデルの実装について説明します。 以下の手順に示すスクリプトは 、 main.py — GitHu b リポジトリに存在し、「 ディープラーニング の詳細」サンプル リポジトリ からフォークされたものです。コード サンプルはディレクトリ内にあります pytorch 。
回帰の例では、次のものが必要です。
- パイソン3
- システムにインストールされている PyTorch モジュール (
pip install torch) - NumPyモジュール(
pip install numpy)がインストールされています - 必要に応じて、エディター (この例では VS Code が使用されています)
問題の説明
前述のように、線形回帰は解析的に解決可能です。 ディープラーニングを使用してこの問題を解決しているのは、トレーニングデータの有効性をすばやく開始して簡単に確認できるためです。 これにより、トレーニング データがデータ セットと比較されます。
Python と PyTorch を使用して次のことを試みます。
- 重みとバイアスを認識した合成データの作成
- PyTorch フレームワークと組み込み関数を使用して、テンソル演算、データセットの読み込み、モデル定義、トレーニングを行う
この例では、グラウンドトゥルースがすでにあるため、検証セットは必要ありません。 合成データの作成中に使用された重みとバイアス値に対する誤差を測定することにより、結果を評価します。
ステップ 1: ライブラリと名前空間をインポートする
単純な線形回帰では、Python でライブラリを torch インポートします。 また、トーチインポートからいくつかの特定の名前空間を追加します。 これは、よりクリーンなコードを作成するのに役立ちます。
# Step 1 import libraries and namespaces import torch from torch.utils import data # `nn` is an abbreviation for neural networks from torch import nn
ステップ 2: データセットを作成する
わかりやすくするために、この例では、ある程度のバイアスを持つ 2 つの変数間に線形関係を形成することを目的とした合成データセットを作成します。
すなわち、 y = mx + バイアス + ノイズ
#Step 2: Create Dataset #Define a function to generate noisy data def synthetic_data(m, c, num_examples): """Generate y = mX + bias(c) + noise""" X = torch.normal(0, 1, (num_examples, len(m))) y = torch.matmul(X, m) + c y += torch.normal(0, 0.01, y.shape) return X, y.reshape((-1, 1))   true_m = torch.tensor([2, -3.4]) true_c = 4.2 features, labels = synthetic_data(true_m, true_c, 1000)
ここでは、組み込みの PyTorch 関数 torch.normal を使用して、正規分布乱数のテンソルを返します。 また、テンソルとテンソル m X を乗算する関数を使用しており、 torch.matmul Y 再び正規分布しています。
単純な散布図を使用して視覚化すると、データセットは次のようになります。
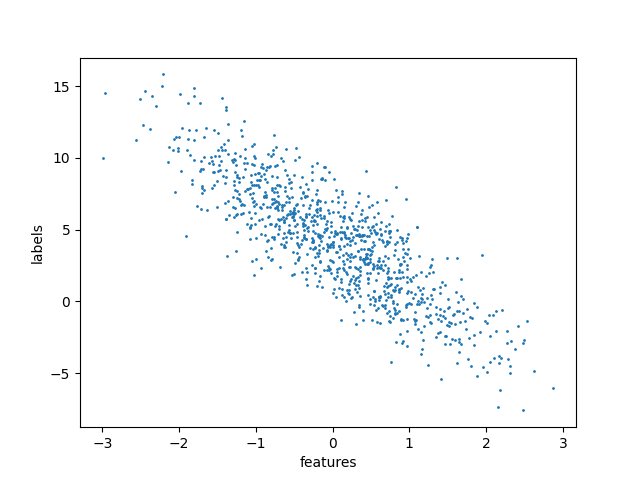
視覚化を作成するコードは、この GitHub リポジトリにあります。
ステップ 3: データセットを読み取り、データの小さなバッチを定義する
#Step 3: Read dataset and create small batch #define a function to create a data iterator. Input is the features and labels from synthetic data # Output is iterable batched data using torch.utils.data.DataLoader def load_array(data_arrays, batch_size, is_train=True): """Construct a PyTorch data iterator.""" dataset = data.TensorDataset(*data_arrays) return data.DataLoader(dataset, batch_size, shuffle=is_train)   batch_size = 10 data_iter = load_array((features, labels), batch_size)   next(iter(data_iter))
ここでは、PyTorch 関数を使用してデータセットを読み取ってサンプリングします。 TensorDataset サンプルとそれに対応するラベルを格納し DataLoader 、アクセスしやすいように を TensorDataset で囲みます。
この iter 関数は Python イテレータを作成し、 next そのイテレータから最初の項目を取得します。
ステップ 4: モデルの定義
PyTorch には、さまざまなケースに対応する事前構築済みのモデルが用意されています。 私たちの場合、2つの入力層と1つの出力層を持つ単層のフィードフォワードネットワークで十分です。 PyTorch のドキュメントには、 nn.linear の実装に関する詳細が記載されています。
このモデルでは、重みとバイアスの初期化も必要です。 このコードでは、平均値が 0、標準偏差値が 0.01 のガウス (正規) 分布を使用して重みを初期化します。 バイアスは単にゼロです。
#Step4: Define model & initialization # Create a single layer feed-forward network with 2 inputs and 1 outputs. net = nn.Linear(2, 1)   #Initialize model params net.weight.data.normal_(0, 0.01) net.bias.data.fill_(0)
ステップ5:損失関数を定義する
損失関数は、二乗平均平方根誤差として定義されます。 損失関数は、データポイントが回帰直線からどれだけ離れているかを示します。
#Step 5: Define loss function # mean squared error loss function loss = nn.MSELoss()
ステップ 6: 最適化アルゴリズムを定義する
最適化のために、確率的勾配降下法を実装します。
は lr 学習率を表し、トレーニング中の更新ステップを決定します。
#Step 6: Define optimization algorithm # implements a stochastic gradient descent optimization method trainer = torch.optim.SGD(net.parameters(), lr=0.03)
ステップ7:トレーニング
トレーニングには、n エポック (この例では 5 つ) の特殊なトレーニング データを使用し、ミニバッチ機能と対応するラベルを繰り返し使用します。 ミニバッチごとに、次の操作を行います。
- 予測を計算し、損失を計算する
- バックプロパゲーションの実行による勾配の計算
- モデル パラメータの更新
- 各エポック後の損失を計算する
# Step 7: Training
# Use complete training data for n epochs, iteratively using a minibatch features and corresponding label
# For each minibatch:
#   Compute predictions by calling net(X) and calculate the loss l
#   Calculate gradients by running the backpropagation
#   Update the model parameters using optimizer
#   Compute the loss after each epoch and print it to monitor progress
num_epochs = 5
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X) ,y)
trainer.zero_grad() #sets gradients to zero
l.backward() # back propagation
trainer.step() # parameter update
l = loss(net(features), labels)
print(f'epoch {epoch + 1}, loss {l:f}')
業績
最後に、真の値をトレーニング済みのモデル パラメーターと比較してエラーを計算します。 誤差値を小さくすることが望ましい。 次のコードスニペットを使用して結果を計算できます。
#Results
m = net.weight.data
print('error in estimating m:', true_m - m.reshape(true_m.shape))
c = net.bias.data
print('error in estimating c:', true_c - c)
コードを実行すると、ターミナルウィンドウに次の情報が出力されます。
パイソン3 main.py 特徴: テンソル([1.4539, 1.1952]) ラベル: テンソル([3.0446])エポック1、損失0.000298 エポック2、損失0.000102 エポック3、損失0.000101 エポック4、損失0.000101 エポック5、損失0.000101 M の推定誤差: テンソル([0.0004, 0.0005]) C の推定中にエラーが発生しました: テンソル([0.0002])
ご覧のとおり、エラーは値とともに徐々に縮小します。
スクリプトのコンテナ化
前の例では、単純なスクリプトを実行するためだけに複数の Python パッケージをインストールする必要がありました。 一方、コンテナーを使用すると、すべての依存関係をイメージに簡単にパッケージ化してアプリケーションを実行できます。
スクリプトをすばやく簡単に Docker 化する方法を紹介します。 ブログのパート 2 では、コンテナー化されたデプロイについて詳しく説明します。
スクリプトをコンテナー化する
コンテナーは、分離された環境でアプリケーションを実行するために必要なコード、依存関係、ライブラリをバンドルするのに役立ちます。 線形回帰スクリプトの簡単なワークフローに取り組みましょう。
これは、Docker デスクトップを使用して実現します。 Docker Desktop には、イメージの全体的なコンテンツを指定する Dockerfiles が組み込まれています。
この例では、必ずPythonベースイメージ(バージョン3.10)をプルしてください。
パイソンから:3.10
次に、コードの実行に必要な and torch 依存関係をインストールします numpy 。
RUN apt update & apt install -y python3-pip
実行pip3インストールナンピートーチ
その後、スクリプトをディレクトリに配置する main.py 必要があります。
コピー main.py アプリ/
最後に、CMD命令は重要な実行可能ファイルを定義します。 この例では、スクリプトを実行します main.py 。
CMD ["python3", "app/main.py" ]
私たちの完全性 Dockerfile を以下に示します、そしてこの GitHubリポジトリ内に存在します:
パイソンから:3.10
RUN apt update & apt install -y python3-pip
実行pip3インストールナンピートーチ
コピー main.py アプリ/
CMD ["python3", "app/main.py" ]
ドッカー イメージをビルドする
Docker Desktop がイメージをビルドするために必要なすべての命令がわかったので、次の手順に従ってイメージを作成します。
- GitHub リポジトリでは、サンプル スクリプトと
Dockerfileが というディレクトリpytorchにあります。リポジトリのホームフォルダから、正しいディレクトリにアクセスするために入力cd deeplearning-docker/pytorchできます。 - 私たちのドッカーイメージは名前が付けられています
linear_regression。 イメージをビルドするには、docker build -t linear_regression. 命令。
ドッカーイメージを実行する
イメージができたので、次のコマンドを使用してコンテナーとして実行できます。
ドッカー実行linear_regression
このコマンドは、コンテナーを作成し、 main.py スクリプトを実行します。 コンテナーを実行すると、損失と見積もりが再出力されます。 これらのコマンドを実行すると、コンテナーは自動的に終了します。 コンテナーの状態は、Docker デスクトップのコンテナー インターフェイスを使用して表示できます。
デスクトップには、コマンドを実行して正常に終了したこと linear_regression が表示されます。
エラーの見積もりは、ターミナルを介して、またはDockerデスクトップ内で直接表示できます。 ログエクスプローラー と呼ばれる Docker拡張機能 を使用して、コンテナの出力を表示しました(以下を参照)。
または、このブログで作成した Dockerイメージ を使用して実験することもできます。
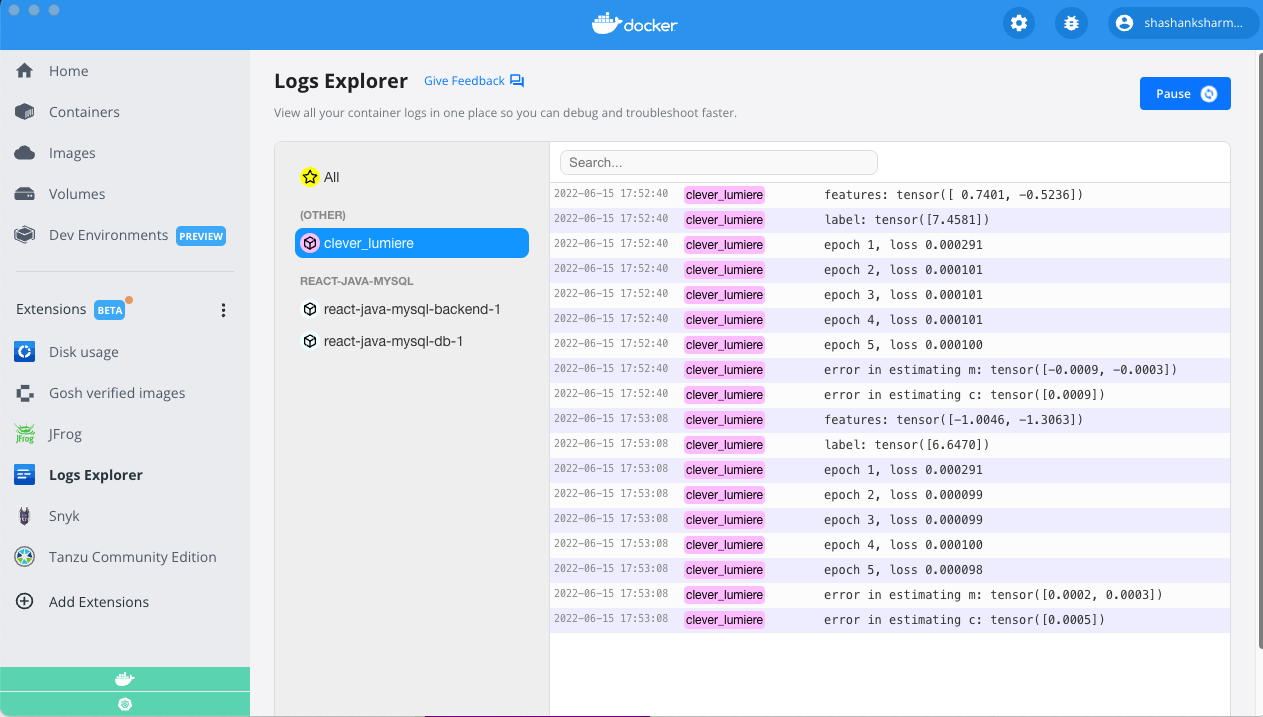
ご覧のとおり、私のシステムとコンテナ内でスクリプトを実行した結果は同等です。
Python でのコンテナーの使用の詳細については、次の役立つリンクを参照してください。
PyTorch の理論と例について詳しく知りたいですか?
私たちは、Python、PyTorch、ディープラーニングの世界を非常に簡単に覗いてみました。 ただし、詳細を知りたい場合は、多くのリソースを利用できます。 ここにいくつかの素晴らしい出発点があります:
さらに、YouTube、Udemy、CourseraなどのWebサイトには、無限の無料および有料コースが存在します。
結論
このブログでは、PyTorch と線形回帰について説明し、PyTorch フレームワークを使用して非常に単純な線形回帰問題を解決しました。 また、PyTorch アプリケーションをコンテナー化する非常に簡単な方法も示しました。